Что такое число Пи простым языком и интересные факты о нем
Число Пи. Символ / sufler1214 марта мир отмечает День числа Пи, так как в этой дате месяц и число образуют то самое π – 3.14. Исходя из этой же логики, начинать праздновать в этот день нужно непременно в 1 час и 59 минут дня.
Главред узнал, чем же это число так важно и интересно.
Как получить число Пи
Число Пи – это отношение длины окружности к ее диаметру и оно является математической константой. Если говорить о том, что такое число Пи простым языком, то можно сформулировать так: если диаметр окружности принять за единицу, то длина окружности и является числом Пи.
Практическое применение числа Пи изначально было связано со строительством. К примеру, проект Великой пирамиды Египта в Гизе разработан на основе числа Пи. Напомним, что построена она была еще в 2589-2566 годах до нашей эры.
Число Пи: чему равно
У разных народов в разное время у числа Пи были разные значение: в Древнем Египте, к примеру, оно равнялось 3,1604, в Китае – 3,1459, в Индии – 3,162.
Более точно π начали высчитывать после появления компьютера. И теперь можно сказать, что число Пи бесконечно, ведь оно насчитывает более 4 млрд знаков.
Число Пи: чему равноКто придумал число Пи
Читайте такжеПисательница сказала, на какие праздники в Украине стоит сделать выходныеЧислу Пи более 4 тысяч лет. По легенде, его использовали еще при возведении Вавилонской башни. Активно пользовались и древние шумеры. Поэтому трудно сказать, кто открыл число Пи. Впрочем, считается, что первым предложил математический способ вычисления древнегреческий ученый Архимед.
Число Пи: интересные факты
1. Несмотря на свой весьма преклонный возраст, свое буквенное обозначение число Пи получило лишь в 1706 году – в честь начальных букв двух греческих слов, означающих окружность и периметр. Число наделил буквой π математик Джонс, а прочно вошла она в математический обиход уже в 1737 году.
2. Существует литературоведческий диалект – Pilish. В нем число букв в последовательно идущих словах соответствует цифре числа Пи. К примеру, Майк Кейт свою книгу «НеWake» полностью написал на языке этого уникального числа.
3. 14 марта, в день числа Пи, родился выдающийся ученый Альберт Эйнштейн и умер Стивен Хокинг, другой великий ученый.
glavred.info
Число «Пи»
14 мар 2012
14 марта математики отмечают один из самых необычных праздников — Международный день числа «Пи». Эта дата выбрана неслучайно: числовое выражение π (Пи) — 3,14 (3 месяц (март) 14 число).
Впервые с этим необычным числом школьники сталкиваются уже в младших классах при изучении круга и окружности. Число π — математическая константа, которая выражает отношение длины окружности к длине ее диаметра. Т.е если взять окружность с диаметром равным единице, то длина окружности и будет равна числу «Пи». Число π имеет бесконечную математическую продолжительность, но в повседневных вычислениях используют упрощенное написание числа, оставляя только два знака после запятой, — 3,14.
В 1987 году этот день отмечался впервые. Физик Ларри Шоу из Сан-Франциско заметил, что в американской системе записи дат (месяц / число) дата 14 марта — 3/14 совпадает с числом π (π = 3,1415926…). Обычно празднования начинаются в 1:59:26 дня (π = 3,14
История числа «Пи»
Предполагается, что история числа π начинается в Древнем Египте. Египетские математики определяли площадь круга диаметром Dкак (D-D/9)2. Из данной записи видно, что в то время число π приравнивали к дроби (16/9)2, или 256/81, т.е. π 3,160…
В VI в. до н.э. в Индии в религиозной книге джайнизма есть записи, свидетельствующие о том, что число π в то время принимали равным квадратному корню из 10, что даёт дробь 3,162…
В III в. до н.э.Архимед в своей небольшой работе «Измерение круга» обосновал три положения:
- Всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и её радиусу;
- Площади круга относятся к квадрату, построенному на диаметре, как 11 к 14;
- Отношение любой окружности к её диаметру меньше 3 1/7 и больше 3 10/71.
Последнее положение Архимед обосновал последовательным вычислением периметров правильных вписанных и описанных многоугольников при удвоении числа их сторон. По точным расчётам Архимеда отношение окружности к диаметру заключено между числами 3*10 / 71и 3*1/7, а это означает, что число «пи» равно 3,1419… Истинное значение этого отношения 3,1415922653…
Впервой половине XV в. астроном и математикал-Каши вычислил π с 16 десятичными знаками.
Спустя полтора столетия в Европе Ф.Виетнашёл число π только с 9 правильными десятичными знаками: он сделал 16 удвоений числа сторон многоугольников. Ф.Виетпервым заметил, что π можно отыскать, используя пределы некоторых рядов. Это открытие имело большое значение, оно позволило вычислить π с какой угодно точностью.
В 1706 г английский математик У.Джонсон ввёл обозначение отношения длины окружности к диаметру и обозначил его современным символом π первой буквой греческого слова periferia—окружность.
На протяжении длительного периода времени учёные всего мира пытались разгадать тайну этого загадочного числа.
В чем же сложность вычисления значения π ?
Число π является иррациональным: его невозможно выразить в виде дроби p/q, где p и q целые числа, данное число не может быть корнем алгебраического уравнения. Нельзя указать алгебраическое или дифференциальное уравнение, корнем которого будет π, поэтому данное число называется трансцендентным и вычисляется путём рассмотрения какого-либо процесса и уточняется за счет увеличения шагов рассматриваемого процесса. Множественные попытки просчитать максимальное количество знаков числа π привели к тому, что сегодня, благодаря современной вычислительной технике, можно рассчитать последовательность с точностью в 10 триллионов цифр после запятой.
Цифры десятичного представления числа π достаточно случайны. В десятичном разложении числа можно найти любую последовательность цифр. Предполагают, что в данном числе в зашифрованном виде есть все написанные и ненаписанные книги, любая информация, которую только можно представить, находится в числе π.
Можете сами попробовать разгадать тайну этого числа самостоятельно. Записать число «Пи» полностью, конечно не получится. Но самым любопытным предлагаю рассмотреть первые 1000 знаковчисла π = 3,
Запоминаем число «Пи»
В настоящее время с помощью вычислительной техники вычислено в десять триллионов знаков числа «Пи». Максимальное число цифр, которое смог запомнить человек составляет сто тысяч.
Чтобы запомнить максимальное количество знаков числа «Пи», используют различные стихотворные «запоминалки», в которых слова с определённым количеством букв располагаются в такой же последовательности, как цифры в числе «Пи»: 3,1415926535897932384626433832795…. Для восстановления числа необходимо подсчитать число символов в каждом из слов и записать по порядку.
Вот и знаю я число, именуемое «Пи». Молодец! (7 цифр)
Вот и Миша и Анюта прибежали
Пи узнать число они желали. (11 цифр)
Это я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду. (21 цифра)
Раз у Коли и Арины
Распороли мы перины.
Белый пух летал, кружился,
Куражился, замирал,
Ублажился,
Головную боль старух.
Ух, опасен пуха дух! (25 знаков)
Можно использовать рифмованные строки, которые помогают запомнить нужное число.
Чтобы нам не ошибиться,
Нужно правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть
Если очень постараться,
Можно сразу пи прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять».
Остались вопросы? Хотите знать больше о числе «Пи»?
Первый урок – бесплатно!
Зарегистрироваться
www.tutoronline.ru
Почему так знаменито число ПИ? Клуб почемучек :: Это интересно!
В «Клубе почемучек», который я, к моему огромному сожалению, стала вести очень редко, сегодня урок математики:) И посвящен он числу ПИ. Даже дошкольники, наверное, о нем слышали. Это число очень значительное и очень загадочное.
Выясняли с Катей, почему.
Я, как человек с математическим образованием, прекрасно это знаю, но вот ребенку в 5 классе объяснять — надо найти нужные слова. Ничего такого они в школе еще не проходили…
Ну а если совсем без слов? Я же все-таки по специальности прикладной математик. Мне хочется не теоретически, а руками «пощупать». И детям так понять проще;)
Вот и решили пройти с Катей всю историю исследований в этой области на практике за полчаса!
Мы это занятие приурочили к Международному Дню числа Пи, который празднуется математиками всего мира 14 марта. Почему именно в этот день? Читайте дальше!
А теперь я и с вами поделюсь моим занятием — вдруг ваш почемучка тоже заинтересуется, что такое число ПИ?
Для начала мы с дочкой взяли изучать не абстрактные окружности, а реальные и осязаемые круги из картона. Разной величины, чтобы было объективнее. Просто начертили циркулем и вырезали из бумаги.
Круг как круг, что в нем исследовать? Какие у него могут быть части? Ну есть центр, диаметр…
А еще есть краешек — граница, окружность. Как бы ее измерить?
Задала дочке этот вопрос.
У Кати возникла идея отметить точечку на краю и прокатить круг вдоль линейки — это и будет длина окружности.
Потом решили, что можно круг обернуть ниткой, а потом измерить ее длину — тоже получится длина окружности.
Все померили — результаты записали.
Но каждый кружок в мире не измеришь, нет ли какой закономерности?
Ведь видно же даже без всяких теорем, что чем больше диаметр круга, тем больше длина его окружности!
Попробовали с моей подачи для каждого нашего круга разделить длину окружности на его диаметр. Чтобы посчитать коэффициент.
И тут сюрприз — бац! Надо было видеть лицо Кати))))
Оказалось, что это отношение у всех кругов очень похоже! Какой кружок не возьми — хоть маленький, хоть большой, хоть бумажный, хоть нарисованный, получается число 3 с махоньким хвостиком!
Просто фокус какой-то — мы же кружки специально не подбирали!
Так это и есть знаменитое ПИ?!!!!!
| Вычисления числа ПИ на практике |
| Что такое ПИ? |
Архимед его высчитывал: все колеса в Греции, наверное, перемерил;) На самом деле, он вычислял периметр вписанных и описанных многоугольников. Ну ооочень многоугольников — которые уже почти сосем как круг.
В результате Архимед определил, что к числу ПИ ближе всего подходит дробь 22/7.
Ее теперь называют архимедовым числом.
По легенде Архимед так был увлечен своими вычислениями, что не заметил, когда римские солдаты ворвались в его родной город Сиракузы. И когда римлянин пошел на него с мечем, он только закричал «Не трогай моих кругов!». И был убит (((
Все знают эту грустную историю с самого детства благодаря советскому мультику «Коля, Оля и Архимед». Мы даже с Катей пересмотрели его еще раз.
| Вычисляем отношение длины окружности к ее диаметру |
А сколько потом людей пыталась точно ПИ посчитать! Что только не делали: многоугольники строили, фракталы применяли! И все равно до конца не домерили — оно бесконечным оказалось 🙂
Например, нидерландский математик 16 века Лудольф ванн Цейлен всю жизнь посвятил расчетам числа ПИ и вычислил его 35 знаков после запятой. По его завещанию, это число выгравировали на его надгробии после смерти.
Вот как оно выглядело 3,1415926535 8979323846 2643383279 50288…
Удивительно, правда? Окружность вполне конечна. А если разделить длину на диаметр, то точную длину не поймаешь!
Люди отчаялись и решили так и записать — просто буквой. Греческой ПИ.
Чтобы не считать каждый раз;)
Первым предложил такое обозначение английский математик Джонс (или в другом написании Джонсон) в 1706 г. Но такое обозначение стало общепринятым через несколько десятков лет (с 1737 года) после работ другого математика — Леонарда Эйлера.
| Коротко о числе ПИ |
Теперь мы знаем, что число это иррациональное. Так говорят на языке математики. Это означает, что оно бесконечное. Это доказал 18 веке математик Иоганн Генрих Ламберт.
Только упертые компьютеры продолжают считать — уже несколько миллионов знаков после запятой вычислили. И дальше стараются:) Но на то они и машины, чтобы работать!
А зачем же это число вообще нужно считать? Какая его практическая ценность?
Число ПИ используется в формулах движения. Оно нужно, чтобы знать, как движутся звезды и планеты, рассчитывать траекторию космических кораблей и орбиты спутников. Его точность важна и в микромире — для вычисления электронных орбит в квантовой физике и квантовой химии. ПИ входит в формулы теории вероятностей, электроники, электротехники, статистики, метеорологии, навигации и многих других областей науки.
Поэтому его и нужно брать как можно точнее.
Но сами же ученые говорят, что на практике трудно найти области, где пригодится точность числа ПИ большая, чем 20 знаков после запятой.
Ну а мы с Катей в своих измерениях будем использовать просто число 3. Этой точности вполне хватает для бытовых нужд.
Хотя дочка на всякий случай еще несколько цифр после запятой выучила: 3,1415926
Стишок для запоминания — на фото!| Мнемоническое правило для запоминания цифр в числе ПИ |
А можно еще запомнить, используя простые МНЕМОНИЧЕСКИЕ ПРАВИЛА.
В этих фразах число букв в каждом слове соответствует цифре в записи числа ПИ
Те, что ниже, приведены в книгах знаменитого математика и популяризатора науки Якова Перельмана.
Что я знаю о кругах? (3.1415)
Вот и знаю я число, именуемое Пи — Молодец! (3.1415926 — округленно)
Учи и знай в числе известном за цифрой цифру, как удачу примечать! (3.14159265359)
Ну и напоследок шуточное стихотворение, построенное на игре слов. Про Математика и Козлика из сказки «Алиса в Стране Чудес», которую написал тоже математик Льюис Кэрролл. Стихотворение люблю с детства в переводе Бориса Заходера:)
| Стихотворение Льюиса Кэрролла, посвященное числу ПИ |
Загляните, там много интересного:)
Кроме того, у меня в блоге есть целых два математических лэпбука — наглядных пособия, которые помогут детям полюбить математику.
Первый для малышей, только изучающих цифры Лэпбук о цифрах: Цифры в стихах, пословицах, загадках»Хотя мы его как ни странно делали для школы в 3 классе на проект «Математичка вокруг нас»
И второй для школьников Лэпбук «История математики», в котором рассказано про то, как математика начиналась: про арабские и римские цифры, про шумеров и египтян и многое-многое другое.
А еще у меня в блоге много материалов для детей, так или иначе касающихся математики. Посмотреть их можно тут:
www.tavika.ru
9 удивительных фактов о числе Пи
Увлеченные математикой люди по всему миру ежегодно съедают по кусочку пирога четырнадцатого марта – ведь это день числа Пи, самого известного иррационального числа. Эта дата напрямую связана с числом, первые цифры которого 3,14. Пи – это соотношение длины окружности к диаметру. Так как оно иррациональное, записать его в виде дроби невозможно. Это бесконечно длинное число. Его обнаружили тысячи лет назад и с тех пор постоянно изучают, но остались ли у Пи какие-нибудь секреты? От древнего происхождения до неопределенного будущего вот несколько наиболее интересных фактов о числе Пи.
Запоминание Пи
Рекорд в запоминании цифр после запятой принадлежит Раджвиру Мине из Индии, которому удалось запомнить 70 000 цифр – он поставил рекорд двадцать первого марта 2015 года. До этого рекордсменом был Чао Лу из Китая, которому удалось запомнить 67 890 цифр – этот рекорд был поставлен в 2005-м. Неофициальным рекордсменом является Акира Харагучи, записавший на видео свое повторение 100 000 цифр в 2005-м и не так давно опубликовавший видео, где ему удается вспомнить 117 000 цифр. Официальным рекорд стал бы только в том случае, если бы это видео было записано в присутствии представителя книги рекордов Гиннеса, а без подтверждения он остается лишь впечатляющим фактом, но не считается достижением. Энтузиасты математики любят заучивать цифру Пи. Многие люди используют различные мнемонические техники, к примеру стихи, где количество букв в каждом слове совпадает с цифрами Пи. В каждом языке существуют свои варианты подобных фраз, которые помогают запомнить как первые несколько цифр, так и целую сотню.
Существует язык Пи
Увлеченные литературой математики изобрели диалект, в котором число букв во всех словах соответствует цифрам Пи в точном порядке. Писатель Майк Кит даже написал книгу Not a Wake, которая полностью создана на языке Пи. Энтузиасты такого творчества пишут свои произведения в полном соответствии количества букв значению цифр. Это не имеет никакого прикладного применения, но является достаточно распространенным и известным явлением в кругах увлеченных ученых.
Экспоненциальный рост
Пи — это бесконечное число, поэтому люди по определению не смогут никогда установить точные цифры этого числа. Однако количество цифр после запятой сильно увеличилось со времен первого использования Пи. Еще вавилоняне им пользовались, но им было достаточно дроби в три целых и одну восьмую. Китайцы и создатели Ветхого Завета и вовсе ограничивались тройкой. К 1665 году сэр Исаак Ньютон вычислил 16 цифр Пи. К 1719 году французский математик Том Фанте де Ланьи вычислил 127 цифр. Появление компьютеров радикальным образом улучшило знания человека о Пи. С 1949 года по 1967-й количество известных человеку цифр стремительно выросло с 2037 до 500 000. Не так давно Петер Труэб, ученый из Швейцарии, смог вычислить 2,24 триллиона цифр Пи! На это потребовалось 105 дней. Разумеется, это не предел. Вполне вероятно, что с развитием технологий будет возможно установить еще более точную цифру — так как Пи бесконечно, предела точности просто не существует, и ограничить ее могут лишь технические особенности вычислительной техники.
Вычисление Пи вручную
Если вы хотите найти число самостоятельно, вы можете использовать старомодную технику – вам потребуются линейка, банка и веревка, можно также использовать транспортир и карандаш. Минус использования банки в том, что она должна быть круглой, и точность будет определяться тем, насколько хорошо человек может наматывать веревку вокруг нее. Можно нарисовать окружность транспортиром, но и это требует навыков и точности, так как неровная окружность может серьезно исказить ваши измерения. Более точный метод предполагает использование геометрии. Разделите круг на множество сегментов, как пиццу на кусочки, а потом вычислите длину прямой линии, которая превратила бы каждый сегмент в равнобедренный треугольник. Сумма сторон даст приблизительное число Пи. Чем больше сегментов вы используете, тем более точным получится число. Разумеется, в своих вычислениях вы не сможете приблизиться к результатам компьютера, тем не менее эти простые опыты позволяют более детально понять, что вообще представляет собой число Пи и каким образом оно используется в математике.
Открытие Пи
Древние вавилоняне знали о существовании числа Пи уже четыре тысячи лет назад. Вавилонские таблички исчисляют Пи как 3,125, а в египетском математическом папирусе встречается число 3,1605. В Библии число Пи дается в устаревшей длине – в локтях, а греческий математик Архимед использовал для описания Пи теорему Пифагора, геометрическое соотношение длины сторон треугольника и площади фигур внутри и снаружи кругов. Таким образом, можно с уверенностью сказать, что Пи является одним из наиболее древних математических понятий, хоть точное название данного числа и появилось относительно недавно.
Новый взгляд на Пи
Еще до того, как число Пи стали соотносить с окружностями, у математиков уже было множество способов даже для наименования этого числа. К примеру, в старинных учебниках по математике можно найти фразу на латыни, которую можно грубо перевести как «количество, которое показывает длину, когда на него умножается диаметр». Иррациональное число прославилось тогда, когда швейцарский ученый Леонард Эйлер использовал его в своих трудах по тригонометрии в 1737 году. Тем не менее греческий символ для Пи все еще не использовали – это произошло только в книге менее известного математика Уильяма Джонса. Он использовал его уже в 1706 году, но это долго оставалось без внимания. Со временем ученые приняли такое наименование, и теперь это наиболее известная версия названия, хотя прежде его называли также лудольфовым числом.
Нормальное ли число Пи?
Число Пи определенно странное, но насколько оно подчиняется нормальным математическим законам? Ученые уже разрешили многие вопросы, связанные с этим иррациональным числом, но некоторые загадки остаются. К примеру, неизвестно, насколько часто используются все цифры – цифры от 0 до 9 должны использоваться в равной пропорции. Впрочем, по первым триллионам цифр статистика прослеживается, но из-за того, что число бесконечное, доказать точно ничего невозможно. Есть и другие проблемы, которые пока ускользают от ученых. Вполне возможно, что дальнейшее развитие науки поможет пролить на них свет, но на данный момент это остается за пределами человеческого интеллекта.
Пи звучит божественно
Ученые не могут ответить на некоторые вопросы о числе Пи, тем не менее с каждым годом они все лучше понимают его суть. Уже в восемнадцатом веке была доказана иррациональность этого числа. Кроме того, было доказано, что число является трансцендентным. Это означает, что нет определенной формулы, которая позволила бы подсчитать Пи с помощью рациональных чисел.
Недовольство числом Пи
Многие математики просто влюблены в Пи, но есть и те, кто считает, что у этих цифр нет особенной значимости. Кроме того, они уверяют, что число Тау, которое в два раза больше Пи, более удобное в использовании как иррациональное. Тау показывает связь длины окружности и радиуса, что, по мнению некоторых, представляет более логичный метод исчисления. Впрочем, однозначно определить что-либо в данном вопросе невозможно, и у одного и у другого числа всегда будут сторонники, оба метода имеют право на жизнь, так что это просто интересный факт, а не повод думать, что пользоваться числом Пи не стоит.
Нашли нарушение? Пожаловаться на содержание
fb.ru
ЧИСЛО ПИ | Энциклопедия Кругосвет
ЧИСЛО p – отношение длины окружности к ее диаметру, – величина постоянная и не зависит от размеров окружности. Число, выражающее это отношение, принято обозначать греческой буквой 241 (от «perijereia» – окружность, периферия). Это обозначение стало употребительным после работы Леонарда Эйлера, относящейся к 1736, однако впервые оно было употреблено Уильямом Джонсом (1675–1749) в 1706. Как и всякое иррациональное число, оно представляется бесконечной непериодической десятичной дробью:
p = 3,141592653589793238462643… Нужды практических расчетов, относящихся к окружностям и круглым телам, заставили уже в глубокой древности искать для 241 приближений с помощью рациональных чисел. Сведения о том, что окружность ровно втрое длиннее диаметра, находятся в клинописных табличках Древнего Междуречья. Такое же значение числа p есть и в тексте Библии: «И сделал литое из меди море, – от края до края его десять локтей, – совсем круглое, вышиною в пять локтей, и снурок в тридцать локтей обнимал его кругом» (3 Цар. 7. 23). Так же считали и древние китайцы. Но уже во 2 тыс. до н.э. древние египтяне пользовались более точным значением числа 241, которое получается из формулы для площади круга диаметра d:
.
Этому правилу из 50-й задачи папируса Райнда соответствует значение 4(8/9)2» 3,1605. Папирус Райнда, найденный в 1858, назван так по имени его первого владельца, его переписал писец Ахмес около 1650 до н.э., автор же оригинала неизвестен, установлено только, что текст создавался во второй половине 19 в. до н.э. Хотя каким образом египтяне получили саму формулу, из контекста неясно. В так называемом Московском папирусе, который был переписан неким учеником между 1800 и 1600 до н.э. с более древнего текста, примерно 1900 до н.э., есть еще одна интересная задача о вычислении поверхности корзины «с отверстием 4½». Неизвестно, какой формы была корзина, но все исследователи сходятся во мнении, что и здесь для числа p берется то же самое приближенное значение 4(8/9)2.
Чтобы понять, каким образом древние ученые получили тот или иной результат, нужно попытаться решить задачу, используя только знания и приемы вычислений того времени. Именно так поступают исследователи старинных текстов, однако решения, которые им удается найти, вовсе не обязательно «те самые». Очень часто для одной задачи предлагается несколько вариантов решения, каждый может выбрать себе по вкусу, однако никто не может утверждать, что именно им пользовались в древности. Относительно площади круга кажется правдоподобной гипотеза А.Е.Раик, автора многочисленных книг по истории математики: площадь круга диаметра d сравнивается с площадью описанного вокруг него квадрата, из которого по очереди удаляются малые квадраты со сторонами 
и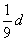 
(рис. 1). В наших обозначениях вычисления будут выглядеть так: в первом приближении площадь круга S равна разности между площадью квадрата со стороной d и суммарной площадью четырех малых квадратов А со стороной 
d:
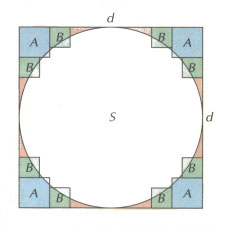
Далее из полученной площади нужно вычесть площадь восьми квадратов B со стороной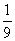 
d, и тогда площадь круга будет приближенно равна следующему выражению:
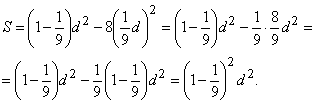
В пользу этой гипотезы свидетельствуют аналогичные вычисления в одной из задач Московского папируса, где предлагается сосчитать
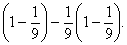
С 6 в. до н.э. математика стремительно развивалась в Древней Греции. Именно древнегреческие геометры строго доказали, что длина окружности пропорциональна ее диаметру (l = 2 p R; R – радиус окружности, l – ее длина), а площадь круга равна половине произведения длины окружности и радиуса:
S = ½ l R = p R2.
Эти доказательства приписывают Евдоксу Книдскому и Архимеду.
В 3 в. до н.э. Архимед в сочинении Об измерении круга вычислил периметры вписанных в окружность и описанных около нее правильных многоугольников (рис. 2) – от 6- до 96-угольника. Таким образом он установил, что число p находится между 3 10/71 и 3 1/7, т.е. 3,14084 < p < 3,14285. Последнее значение до сих пор используется при расчетах, не требующих особой точности. Более точное приближение 3 17/120 (p » 3,14166) нашел знаменитый астроном, создатель тригонометрии Клавдий Птолемей (2 в.), но оно не вошло в употребление.
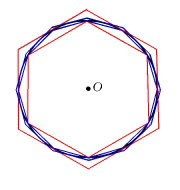
Индийцы и арабы полагали, что p =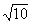 
. Это значение приводит так же и индийский математик Брахмагупта (598 – ок. 660). В Китае ученые в 3 в. использовали значение 3 7/50, которое хуже приближения Архимеда, но во второй половине 5 в. Цзу Чун Чжи (ок. 430 – ок. 501) получил для p приближение 355/113 (p » 3,1415927). Оно осталось неизвестно европейцам и было вновь найдено нидерландским математиком Адрианом Антонисом только в 1585. Это приближение дает ошибку лишь в седьмом десятичном знаке.
Поиски более точного приближения p продолжались и в дальнейшем. Например, аль-Каши (первая половина 15 в.) в Трактате об окружности (1427) вычислил 17 десятичных знаков p. В Европе такое же значение было найдено в 1597 году. Для этого ему пришлось вычислять сторону правильного 800 335 168-угольника. Нидерландский ученый Лудольф Ван Цейлен (1540–1610) нашел для него 32 правильных десятичных знака (опубликовано посмертно в 1615), это приближение называется лудольфовым числом.
Число p появляется не только при решении геометрических задач. Со времени Ф.Виета (1540–1603) разыскание пределов некоторых арифметических последовательностей, составляемых по простым законам, приводило к тому же числу p. В связи с этим в определении числа p принимали участие почти все известные математики: Ф.Виет, Х.Гюйгенс, Дж.Валлис, Г.В.Лейбниц, Л.Эйлер. Они получали различные выражения для 241 в виде бесконечного произведения, суммы ряда, бесконечной дроби.
Например, в 1593 Ф.Виет (1540–1603) вывел формулу
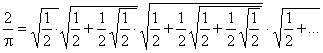
В 1658 англичанин Уильям Броункер (1620–1684) нашел представление числа p в виде бесконечной непрерывной дроби
,
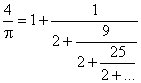однако неизвестно, как он пришел к этому результату.
В 1665 Джон Валлис (1616–1703) доказал, что
,
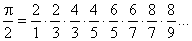или
.
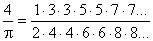Эта формула носит его имя. Для практического нахождения числа 241 она мало пригодна, но полезна в различных теоретических рассуждениях. В историю науки она вошла как один из первых примеров бесконечных произведений.
Готфрид Вильгельм Лейбниц (1646–1716) в 1673 установил следующую формулу:
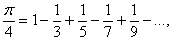
выражающую число p /4 как сумму ряда. Однако этот ряд сходится очень медленно. Чтобы вычислить p с точностью до десяти знаков, потребовалось бы, как показал Исаак Ньютон, найти сумму 5 млрд чисел и затратить на это около тысячи лет непрерывной работы.
Лондонский математик Джон Мэчин (1680–1751) в 1706, применяя формулу
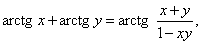
получил выражение
arctg 1 = 4 arctg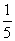 
– arctg 
.
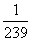Подстановка в него arctg 1 =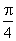 
и рядов для arctg x (arctg x = 
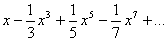) приводит к формуле
,
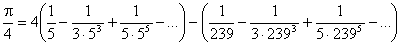которая до сих пор считается одной из лучших для приближенного вычисления p. Чтобы найти те же десять точных десятичных знаков, потребуется всего несколько часов ручного счета. Сам Джон Мэчин вычислил p со 100 верными знаками.
C помощью того же ряда для arctg x и формулы
p = 24 arctg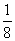 
+ 8 arctg 
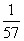+ 4 arctg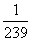
значение числа p было получено на ЭВМ с точностью до ста тысяч десятичных знаков. Такого рода вычисления представляют интерес в связи с понятием случайных и псевдослучайных чисел. Статистическая обработка упорядоченной совокупности указанного количества знаков p показывает, что она обладает многими чертами случайной последовательности.
Есть несколько забавных способов запомнить число p точнее, чем просто 3,14. Например, выучив следующее четверостишие, можно без труда назвать семь десятичных знаков p:
Нужно только постараться
И запомнить все как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
(С.Бобров Волшебный двурог)
Подсчет количества букв в каждом слове следующих фраз так же дает значение числа p:
«Что я знаю о кругах?» (p » 3,1416). Эту поговорку предложил Я.И.Перельман.
«Вот и знаю я число, именуемое Пи. – Молодец!» (p » 3,1415927).
«Учи и знай в числе известном за цифрой цифру, как удачу примечать» (p » 3,14159265359).
Учитель одной из московских школ придумал строку: «Это я знаю и помню прекрасно», а его ученица сочинила забавное продолжение: «Пи многие знаки мне лишни, напрасны». Это двустишие позволяет определить 12 цифр.
А так выглядит 101 знак числа p без округления
3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679.
В наше время с помощью ЭВМ значение числа p вычислено с миллионами правильных знаков, но такая точность не нужна ни в каких вычислениях. А вот возможность аналитического определения числа p имеет принципиальное значение для геометрии. В частности, в неевклидовой геометрии p также входит в некоторые формулы, но уже не как отношение длины окружности к диаметру (в неевклидовой геометрии это отношение не является постоянным).
В окончательном выяснении арифметической природы числа p решающую роль сыграла замечательная формула Эйлера:
e2241i = 1,
где e – основание натуральных логарифмов, i =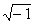 
.
Кстати, Эйлеру принадлежат и другие красивые формулы, включающие 241:
,
,
.
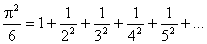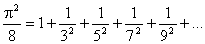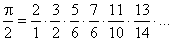В последней формуле в числителе стоят все простые числа, а знаменатели отличаются от них на единицу, причем знаменатель больше числителя, если тот имеет вид 4n + 1, и меньше в противном случае.
Хотя еще с конца 16 в., т.е. с тех пор, как сформировались сами понятия рациональных и иррациональных чисел, многие ученые были убеждены в том, что p – число иррациональное, но только в 1766 немецкий математик Иоганн Генрих Ламберт (1728–1777), основываясь на открытой Эйлером зависимости между показательной и тригонометрической функциями, строго доказал это. Число p не может быть представлено в виде простой дроби, как ни были бы велики числитель и знаменатель.
В 1882 профессор Мюнхенского университета Карл Луиз Фердинанд Линдеман (1852–1939) используя результаты, полученные французским математиком Ш.Эрмитом, доказал, что p – число трансцендентное, т.е. оно не является корнем никакого алгебраического уравнения anxn + an–1xn–1+ … + a1x + a0 = 0 с целыми коэффициентами. Это доказательство поставило точку в истории древнейшей математической задачи о квадратуре круга. Тысячелетия эта задача не поддавалась усилиям математиков, выражение «квадратура круга» стало синонимом неразрешимой проблемы. А все дело оказалось в трансцендентной природе числа p.
В память об этом открытии в зале перед математической аудиторией Мюнхенского университета был установлен бюст Линдемана. На постаменте под его именем изображен круг, пересеченный квадратом равной площади, внутри которого начертана буква p.
Марина Федосова
www.krugosvet.ru
Чему равно число пи в математике
Число пи — самая известная константа в математике. Знаком пи обозначается отношение длины к диаметру окружности. Привычное обозначение константа получила не в Древней Греции, как следовало бы ожидать, а в Британии в 1706г. нашей эры. Математик Джонс в своих расчётах обозначил соотношение длины и диаметра окружности первой буквой греческих слов «периферия» и «периметр».
Чтобы ответить на вопрос, чему равно число пи, необходимо вспомнить некоторые его свойства:
- Константа пи является иррациональной. Значит, пи не может быть выражено в виде простой дроби, где и числитель, и знаменатель являются целыми числами. Из этого следует, что если представить число пи как десятичную дробь, то эта дробь будет не только бесконечной, но и непериодической. Мало того что количество цифр после запятой бесконечно, из него ещё и нельзя выделить постоянно повторяющуюся последовательность.
- Константа пи является трансцендентной. Значит, пи нельзя представить как корень какого-либо многочлена, коэффициенты которого являются целыми числами.
Несмотря на всё вышеперечисленное учёные издревле пытались вычислить значение этой константы.
История вычисления константы пи
Ещё в третьем тысячелетии до нашей эры учёные из Древнего Египта, Месопатамии, Индии и Греции замечали, что соотношение длины и диаметра окружности всегда чуть больше трёх независимо от размеров окружности.
Изучение пи в древней Европе
В Месопотамии это соотношение считали равным трём. В Индии отношение длины к диаметру окружности приравнивали к квадратному корню из десяти. Первым математиком, предложившим доказательный метод расчёта пи, был Архимед. Его способ был прост и нагляден. Архимед вписывал в окружность с диаметром в единицу равносторонние многоугольники и описывал такие же многоугольники вокруг окружности, а потом вычислял периметры этих многоугольников. Таким образом, он получал границы для оценки длины окружности: периметр вписанного многоугольника ограничивал длину окружности снизу, а периметр описанного многоугольника — сверху.
Увеличивая количество углов в многоугольниках, Архимед повышал точность своей оценки. Когда он дошёл до 96 углов в многоугольнике, расчётное значение длины окружности оказалось больше, чем 3+10/71, но меньше, чем 3+1/7. Тогда Архимед выбрал верхнюю границу в качестве приблизительного значения константы пи. Согласно этому предположению, число пи равно 22/7 или 3,142857, если представить его в виде десятичной дроби. То есть, Архимед приблизился к числу пи с точностью до второго знака.
Во втором веке нашей эры дело Архимеда продолжил Клавдий Птолемей. Он довёл количество углов в многоугольнике до 720 и получил приблизительное значение числа пи 377/120 или 3,14166667. Клавдию Птолемею удалось высчитать константу пи с точностью до третьей цифры после запятой.
В шестнадцатом веке нашей эры математик из Голландии Лудольф ван Цейлен потратил десять лет на удваивание углов многоугольника и высчитал константу пи с точностью до двадцати знаков после запятой. Он завещал, чтобы найденные им цифры были выбиты на его надгробной плите. А саму константу стали называть числом Лудольфа.
Изучение числа пи в древнем Китае
Наряду с европейскими математиками, число пи пытались рассчитать и в Поднебесной. В третьем веке нашей эры математик из Китая Лю Хуэй вывел алгоритм, для расчёта константы пи с любой возможной степенью точности. В основу алгоритма легла всё та же идея Архимеда. По такому алгоритму самим Лю Хуэем было высчитано приближение пи для многоугольника с 3072 углами. Оно получилось равным 3,14159. Точность возросла до пятого знака после запятой. В пятом веке нашей эры математик Цзу Чунчжи Вычислил пи с точностью до семи цифр после запятой, расположив эту константу между 3,1415926 и 3,1415927.
Число пи: от средневековья до наших дней
В связи с развитием математического анализа во втором тысячелетии нашей эры для нахождения значения числа пи стали использоваться математические ряды:
Ряд Мадхавы-Лейбница сходился медленно, но после некоторых преобразований позволил вычислить константу пи с точностью до одиннадцати цифр после запятой.- Формула Виета — первая точная математическая формула для нахождения числа пи — представляет собой бесконечное произведение.
- Формула Валлиса также представляет собой произведение для расчёта константы пи по аналогии с константой е.
- Формула Джона Мэчина имеет в своей основе разложение арктангенса в Ряд Тейлора.
- Бесконечный ряд обратных квадратов, как доказал Эйлер сходится к квадрату пи, деленному на шесть.
Ряд Мадхавы-Лейбница сходился медленно, но после некоторых преобразований позволил вычислить константу пи с точностью до одиннадцати цифр после запятой.Теория вероятностей тоже внесла свой вклад в вычисление пи с помощью метода Монте-Карло и Иглы Бюффона. Но с появлением компьютеров, а также открытием преобразования Фурье, использование рядов для вычисления значения пи позволило достигать астрономической точности.
Чему равно число пи?
Если обобщить опыт предков и пересказать его простыми словами, то выяснится, что после запятой константа пи имеет бесконечное множество знаков, среди которых можно встретить абсолютно любую последовательность цифр, и которые не имеет никакой закономерности. Число пи с точностью до ста знаков после запятой будет выглядеть так:
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679.
Последнее зарегистрированное открытие, связанное с числом пи, было сделано в 2016 году. Американец Йи на пару с японцем Кондо высчитал десять триллионов цифр константы. Выучить их все, скорее всего, не удастся. Мировой рекорд по запоминанию цифр константы пи принадлежит индийскому студенту, запомнившему всего семьдесят тысяч знаков.
Сколько цифр из числа пи нужно знать зависит от требуемой точности вычислений. Держать в голове несколько сотен знаков константы пи имеет смысл только для тренировки памяти. Есть он-лайн калькуляторы, позволяющие высчитать пи с любой заданной точностью.
Как запомнить число пи?
Если же хочется держать в памяти более точное значение пи, чем выученные в школе 3,14, то на помощь придут мнемонические правила запоминания. Стишок С. Боброва из произведения «Волшебный двурог» позволяет запомнить число пи с точностью до тринадцати знаков после запятой:
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим — Это будет пять, три, пять,
Восемь, девять, восемь.
Другая разновидность мнемонических правил предлагает запоминать цифры из числа пи, сопоставляя их с количеством букв в каждом из слов стихотворения. Например:
Это я знаю и помню прекрасно,
Но многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду.
Это маленькое четверостишие позволяет вспомнить до двадцати цифр числа пи после запятой.
Видео
liveposts.ru
❶ Что такое число пи 🚩 что значит число пи 🚩 Математика
Пи («π») представляет из себя математическую константу, полученную довольно интересным путем. Допустим, что диаметр окружность равен 1 условной единице. Тогда число π — это длина данной окружности, которая приблизительно равна 3,14 условных единиц. Говоря другими словами, число «пи» выражает соотношение между длиной окружности и ее диаметром. Это соотношение будет всегда постоянным.
Пи обладает рядом свойств.
Во-первых, число π иррационально, это означает, что его нельзя представить в виде правильной дроби. Значение 3,14 является достаточно приблизительным, доподлинно не известно, сколько же знаков после запятой у этой константы.
Во-вторых, число π — трансцендентное. Это означает, что оно никогда не может быть степенью какого-либо корня из другого числа. Говоря иначе, число π не является алгебраическим. Более того, если какое-либо число возвести в степень π, то опять же получится трансцендентное число.
Стоит отметить, что древние математики Египта, Греции, Рима, Сирии и Ирана уже знали, что соотношение между диаметром окружности и ее длиной является постоянной величиной. К примеру, в Вавилоне это соотношение оценивалось как 25/8, а в Египте как 256/81. Но наибольших успехов в вычислении значения числа π добился Архимед, который путем многократного описывания вокруг окружности и вписывания в нее правильных многоугольников добился довольно точных результатов. Периметр вписанного многоугольника Архимед принял за минимальное значение числа π, а описанного — за максимальное. Таким образом, Архимед вывел значение константы π, равное 3.142857142857143.
Забавно отметить, что существует праздник «День числа π», который празднуется 14 марта. Это происходит потому, что если записать числами день и дату праздника, то получится 3.14 — приблизительное значение данной константы. По другой версии, этот праздник надо отмечать 22 июля, так как 22/7 тоже является одним из первых соотношений, приблизительно равным 3.14
www.kakprosto.ru
